Newton Poetry

Newtpocalpyse looks to be a pervasive problem in the Newton community.

All those hopes about Newton users using their eMates and MessagePads past January 5 this year? It’s still possible, just a little annoying now that something else is messing with our Newtons. Several Newtontalkers (here, here, and here) have reported that their 2010-patched Newton 2.x devices, when reset, have their dates revert back to January 1, 2008.

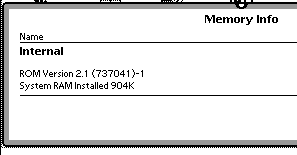
Sure enough, so did my eMate 300. Here it is after I did a test reset:

Before resetting my eMate, I made sure the date and time were correct (something I often neglect after my batteries die). After hitting the reset button, the 2010-to-2008 bug (Y2008?) worked its evil magic. My dates were reset to 2008.

Thankfully, Eckhart Köppen is back on the scene after some time away, and had this to report:

The NewtonOS seems to have built in a “protection” against setting the date to a nonsensical value, which kicks in only after a reset. This protection forces the date to a 1996 on an unpatched Newton.

What happens on a patched Newton is the following sequence (assuming the date is past 2009):

1. Reset occurs
2. NewtonOS notices date after 2009 and sets it back back to 1996
3. Y2010 patch kicks in and sets the time to 2008 (since 1996 is not a valid date once the Newton has been patched)

I have so far not found a good place where to disable step 2, and it might be that this is happening in an unpatchable part of the ROM (step 3 is done in a pretty hackish way already), but I’m trying to get this resolved, because it annoys me as well :)

In the meantime, I would recommend not resetting your Newton if you can help it. If it does happen, simply reset your clock and dates.

And we’ll all wait for Mr. Köppen to fight this dragon, too.

“I had enormous difficulty installing these patches until I read the advice to have as much space as possible on the eMate and the 2100 before trying it, after which it went like clockwork. After several weeks of frustration one feels such an idiot for having ignored that advice, but great relief when it is done. Thanks to everyone who made it possible.”

– Oliver Leaman, sharing his 2010 patch experiences with NewtonTalk. Learn more about the Newtpocalypse, and how it was avoided.

With Eckhart Köppen’s Newtpocalypse patch for the eMate complete, I thought I’d install it and see how it performs on my own Newton eMate.

First, though, I downloaded the new Classilla browser for OS 9. This variation of the old Mozilla browser is getting a lot of attention, and deservedly so. Development on iCab has ceased, and many of the Classic Mac browsers do a poor job of rendering modern web sites.

As a test, I used Classilla to navigate Köppen’s 40Mhz.org site, where he posts his Newton projects, and download the patch from Sourceforge.

It’s easy to install Köppen’s patch. In fact, it’s nothing more than a simple package installation with an automatic reset added at the end. You can either use the Classic Mac installation methods, using Newton Connection Utilities, or the modern NCX or various other OS X-based Newton apps.

I’m using Newton Connection Utilities on an iMac G3 running OS 9, and connecting with a serial-to-USB dongle.

First, download your specific patch file from Köppen’s 40Mhz.org site. As you see above, you’ll have a few options on which patch to download. In my case, I need the 73J186 version.

Above you see that my eMate is running Newton OS 2.1, version 737041. This is the part that’s going to change.

To install Köppen’s Patch 73J186, head to Newton Connection Utilities (on OS 9, or another package installer on OS X) and pick your patch version (above).

Your package installer will upload the patch to your Newton.

After the patch is done installing, your Newton will reset on its own.

After the restart, my eMate shows the Newton OS 2.1, version 73J186 (the same as the patch version) is installed and up to date.

That’s it. And so far, after running my eMate through a battery of high-powered tests (like turning it on and scribbling some notes), everything is hunky-dorey. Bring on 2010.

How did your patching process turn out?

Hip hop hurray.

Newton savior Eckhart Köppen announced yesterday that the Newton eMate and German MessagePad 2100 Year 2010 patches are complete and ready for installation. These patches fix the dreaded Newtpocalypse on Newton OS 2.1 models.

Be sure to download the Y2010 patches at Köppen’s Sourceforge.net project page.

I’ll be running the patch on my own eMate, and will post a breakdown when it’s complete. In the meantime, if you have an MP2x00 or eMate, run these patches yourself and report back to Köppen if you face any troubles.

The entire Newton community appreciates Köppen’s work on this. Thanks to him, and all the volunteers who test the patches, our Newtons will keep running for the foreseeable future.

Eckhart Köppen is looking for testers for his eMate and German MP2100 Year 2010 patch. He says on his blog:

The Y2010 patches for the eMate and German MP2100 are ready, and they seem to work fine here, but I’d still like to give them more testing. Like with the first Y2010 patch, I’m looking for people who can either risk bricking a Newton (with me unbricking it), or who have access to a US MP2x00 to unbrick a Newton themselves via a ROM board swap. Note that I don’t expect any unbricking to be necessary, but you never know.

If you have a spare eMate or Deutschland MessagePad, you can help prevent Newtpocalypse.

Chris Foresman over at Ars Technica does a great job of covering the Newton’s 2010 Patch:

If you are the sort of person who would just as soon have your Newton pried from your cold, dead hand, Köppen’s solution should keep your trusty device in operating condition at least until you or your Newton biodegrades—whichever comes first.

Heed NewtonTalk’s Twitter feed, however, because there are always a few trolls under the bridge.

In fact, these days, I avoid comment sections all together unless the blog or site has a reputation for civil conversation.

Yesterday, the Unofficial Apple Weblog announced that 2010 would be a dire year for Newton users. Some strange Year 2010 bug was bound to make MessagePad fans drown in tears of obsolete sorrow.

It’s too bad TUAW’s Steven Sande jumped the gun, because – as of a few weeks ago – Eckhart Köppen released a patch fixing the Y2010 bug. A quick browse through the Newtontalk list or, shucks, even this modest blog, would’ve brought Köppen’s patch to light.

Sande later fixed his oversight, but attempted to cover his tracks by making fun of Newton users.

“Frankly, considering the caveats listed on the update page, I think it would be a much better idea just to get an iPhone, guys!” he wrote.

Frankly, Steve, we’re doing just fine, thankyouverymuch – even if we don’t qualify as “mainstream consumers.”

What’s weird is that TUAW, at least twice in the last year or so, has reported on this exact same story, offering incremental updates on the situation. Both articles (along with the other Newton articles TUAW has posted, which help to keep the Newton in the public’s eye) are easily found using the blog’s Newton tag.

Do they not discuss Newton matters at the TUAW office before posting on them?

I appreciate that Sande gave an update on his error, but the little dig at the end is what got me.

Also, I can’t help but feel “Newtapocalypse” – as TUAW’s headline reads – sounds clunky. The “a” stuck in the middle adds an unnecessary syllable to the phrase. I much prefer “Newtpocalypse,” if only because it sounds more like the original “apocalypse.”

Four syllables. Rolls off the tongue nicely.

[Thanks to Newtontalk for the heads-up.]

Eckhart Köppen, the whiz behind the Y2010 Diagnostic tool, has come up with a simple four-step process to get rid of the problematic Fix2010 packge:

1. Install the Y2010 Diagnostic Tool
2. Launch the tool and Tap “Clear Alarms” – note, you will lose all alarms in Dates and need to set them again!
3. Delete the Fix2010 patch package
4. Reboot the Newton

Now Köppen is looking for volunteers with MessagePad 2100s to help him work on a solution to the 2010 bug. His patch testing is a four-step process, as well. If you have a spare MP2100, and you want to help contribute to the Y2010 fix, contact Köppen to help with his testing.

Does the Newton’s 2010 bug got you down? Eckhart Köppen, the same Newton developer who created a Wiki on the 2010 bug, has issued a Y2010 Diagnostic application to help relieve some of the symptoms.

Köppen told the NewtonTalk list:

This small application lets you diagnose the content of your soups, and check which kind of alarms you have set. It should clarify what exactly might go wrong in the future instead of second guessing and brain wiping the Newton without proper reason…If you’re hit by an infinite alarm loop, you can if you’re lucky launch the Y2010 Diagnostic app and use it to clear the alarms.

Köppen suggests anyone who installed the problematic Fix2010 patch should remove it, and says that a fix to the whole issue should be out “well in time before 2010.”

[Thanks to NewtonTalk on Twitter.]